Boundary Conditions

Without additional boundary conditions that constrain the wavefield at the boundaries of the computational domain, the wave equation does not obey a unique solution.

All boundary conditions are defined on so-called side sets of the mesh. A side set is just a way to flag edges (in 2D) or faces (in 3D) of a mesh and to give these a name. This is important, whenever different conditions are applied on different parts of the boundary of the domain.

The example mesh below has 4 side sets, each denoting one side of the mesh. The actual names are arbitrary and mesh dependent.

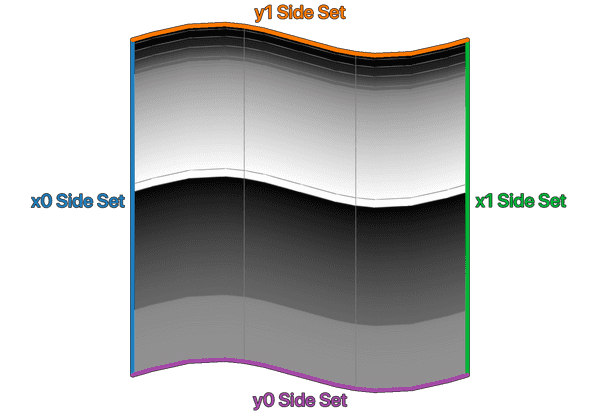
Common defaults for labelling the boundaries are

• for Cartesian meshes: x0, x1, y0, y1, and additionally z0, z1 in 3D,
• for spherical meshes: r0 for the inner radius (if present), r1 for the outer radius,
• for spherical chunks: r0, r1 p0, p1, t0, t1.

In the following, $\Gamma$ denotes a side set where a certain boundary condition is imposed.

Without explicitly specifying boundary conditions, the spectral-element method will fall back to the [natural boundary conditions] (./boundary_conditions/natural_boundary_conditions).