Urgent Computing: The largest Salvus simulation yet
When a devastating earthquake occurs...
In the future, large-scale seismic simulations for urgent computing might assist to answer some of these questions. The ChEESE Center of Excellence in Solid Earth aims to tackle these scientific, computational and socio-economical challenges on upcoming Exascale supercomputers.
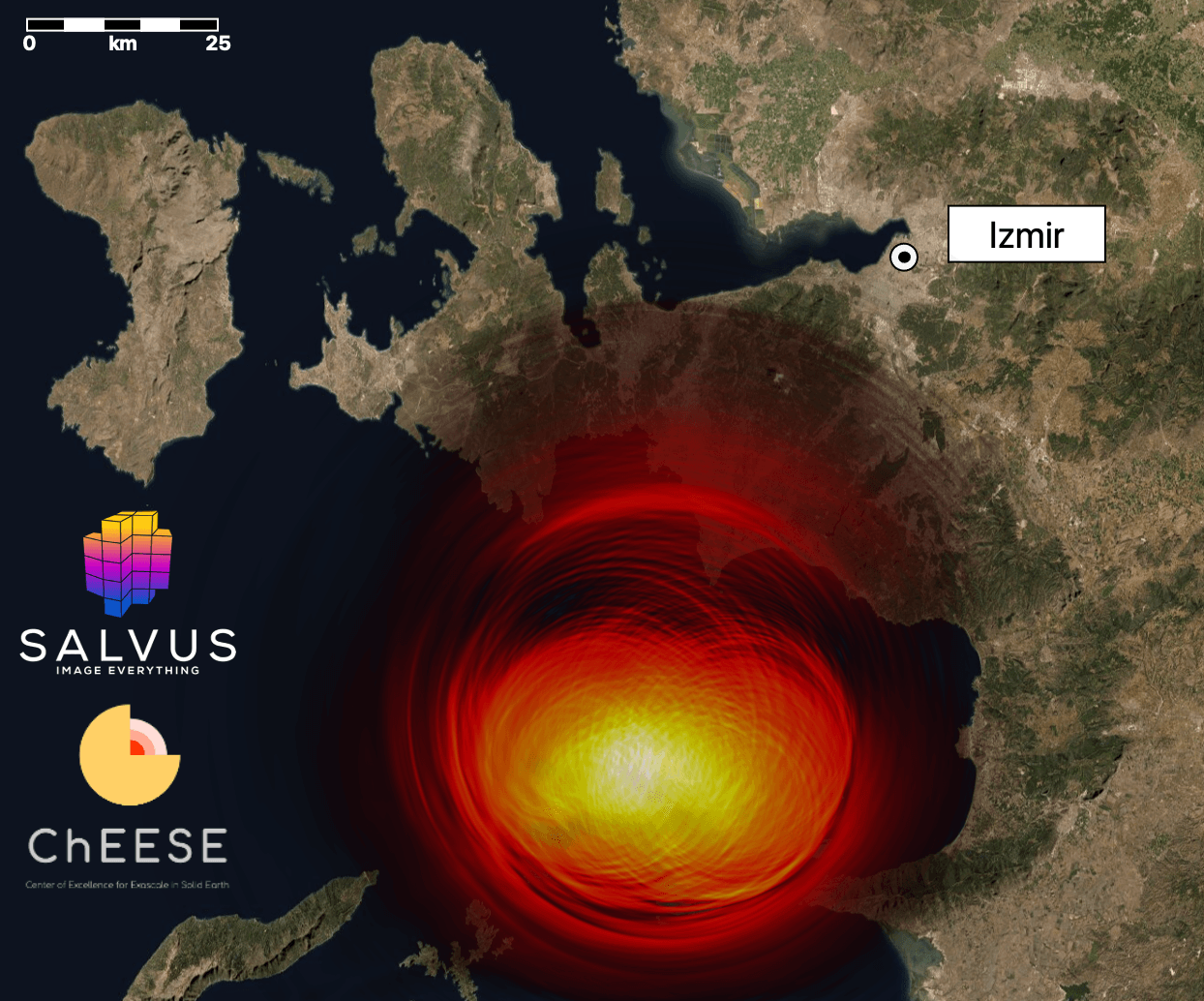
In this context, researchers from ETH Zurich and the Barcelona Supercomputing Center joined forces to simulate the Mw 7 earthquake that struck on October 30, 2020, with the epicenter about 14 km northeast of the Greek island of Samos in the Icarian Sea.
And this turned into the largest Salvus simulation done so far...
Simulation setup
The question raised by the researchers was this: If we had access to an entire supercomputer, which frequencies can we resolve within a few hours of wall-time?
After a succesful grant application, they indeed got access to the full BSC-CNS MareNostrum 4 supercomputer. The challenge was to run a simulation that produces seismograms accurate up to frequencies of 20 Hz including full-waveform physics and realistic 3D Earth structure.
The scenario considers a domain covering an area of about 100 x 100 km at the surface including large parts of the Icarian Sea, the islands Chios and Samos, as well as Izmir and the Turkish coast line. The fault is modeled as a collection of moment-tensor point sources. The Earth model contains 3D Earth structure obtained from previous tomographies as well as realistic topography and bathymetry.
Facts and Figures
To keep the number of elements as small as possible, the researchers used spectral elements of order 7. In the absence of thin layers in the model, higher orders resolve the same frequencies with fewer elements per wavelength and usually outperform lower orders in terms of their cost/accuracy ratio. Each 7-th order element has 512 local grid points. For a visco-elastic simulation, we need to store values for displacement, velocity, and acceleration, as well as the states of the ordinary differential equations that model attenuation. This gives a total of 14 fields at each grid point.
The resulting spectral-element mesh contained almost 215 million elements, which gives more than 1.5 trillion unknowns -- and these are only the space-dependent degrees of freedom. The time integration additionally requires more than 100'000 time steps. Multiplying the degrees of freedom in space and time gives a total of 164 664 116 147 707 904 unknows. That's a lot of number crunching!
A preview of what has been computed after running for several hours on 84'000 MPI ranks is shown in the animation at the top of the page. The animiation depicts several snapshots of the magnitude of the displacement field
At this extreme scale, a very important ingredient is to read and interpolate the spectral-element mesh in parallel. To this end, Salvus heavily relies on PETSc. DMPlex and details can be found in this paper.
Interested in learning more? Futher information can be found in a recent presentation at EGU 2021.
Benefits of Salvus for ambient noise monitoring
- Excellent parallel performance and scalability on high-performance compute clusters.
- Rapid prototyping for a fast transition from small-scale tests to full-production runs.
- Parallel I/O and support for various output quantities.
- Easy visualization of large output volumes.
- Modern Python-based user interface and extendable research platform.
References
- M. Pienkowska et al. (2021): Deterministic modelling of seismic waves in the Urgent Computing context: progress towards a short-term assessment of seismic hazard EGU General Assembly 2021, online, 19–30 Apr 2021, EGU21-15516. doi: 10.5194/egusphere-egu21-15516
- V. Hapla et al. (2021): Fully Parallel Mesh I/O Using PETSc DMPlex with an Application to Waveform Modeling. SIAM Journal on Scientific Computing, 43:2, C127-C153 . doi: 10.1137/20M1332748
 Mondaic
Mondaic