Full-Waveform Near-Surface Site Characterization

Knowing the near-surface structure is of major importance for engineering and construction projects. Improved confidence directly results in reduced risks and associated costs. Seismic surface wave sample that region well and can be routinely acquired.

A large number of methods is being exploited for this purpose. Many of them use approximations of the wave equation to tame algorithmic complexity and computational costs. Utilizing the full wavefield can naturally retrieve more information from the data and Salvus, from the ground up, has been designed to tackle these types of problems.

Surface Wave FWI

Full seismic waveform inversion (FWI) is the natural evolution of approximate surface wave dispersion methods. For this case study we'll apply Salvus' FWI capabilities to a vibroseis field study using real data and highlight a few benefits of using Salvus:

• Built-in data processing and easy access to the full scientific Python stack.
• A wide range of supported misfit functionals.
• Automatic but still flexible full waveform inversion.

Simplistic Data Processing

Data processing can often be the most time consuming part of the full waveform inversion process. Salvus ships with a large number of built-in processing functionality for common aspects. Furthermore, since the whole user-interface is exposed as a Python library, the full power of the world leading data-science Python stack is readily available to attack even the most cutting edge use cases.

Aside from the actual processing being simplified with Salvus, using the full wavefield also directly reduces the need to process in the first place. In fact, for this project, the processing consists only of these four steps, all of which can be performed without manual intervention:

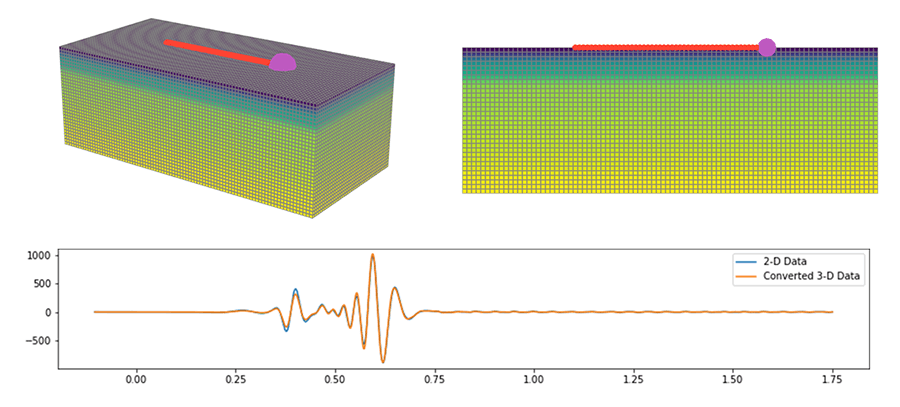
• 3-D to 2-D conversion
• Removing noise before the first arrival
• Bandpass filtering
• Geophone response removal

A single function call for example triggers 3-D data to be converted into its 2-D counterpart. For line deployments this greatly reduces the computational costs because the data can be analyzed with a 2-D digital twin.

Figure: Validation of the point-to-line-source transformation (3-D to 2-D data conversion) using synthetic Salvus simulations. An analytic transform only exists for homogeneous full spaces but the error is acceptable here. The generality of Salvus makes running these types of comparisons a snap.

Full-Trace Optimal Transport Misfit

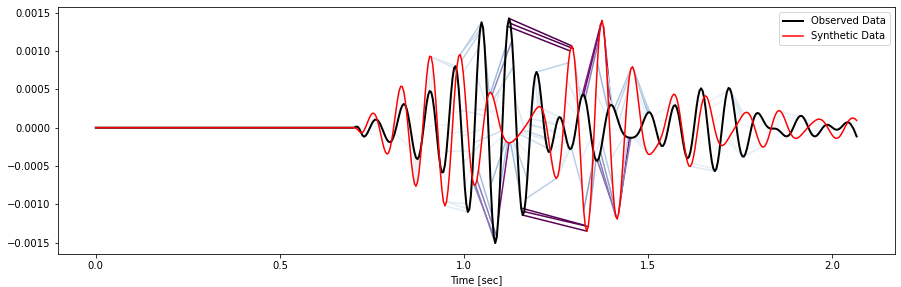
FWI using waveform differences classically suffers from the cycle skipping problem demanding very good starting models. Using different misfit functionals can alleviate that. Salvus comes with a range of user-selectable misfit functions and, in addition, users can define their own misfit measures and directly integrate them into Salvus' inversion machinery.

State-of-the-art research offers several alternatives, one of them being optimal transport in graph-space pioneered in this work. Salvus contains an implementation and it readily enables the usage of the whole trace without worrying about muting the late arrivals.

Figure: A visualization of how the graph-space optimal transport algorithm tries to match pieces of data. The optimization will cause discrete data points in the synthetics to move along the purple lines towards the observed data. This largely eliminates cycle skipping and an iterative inversion is, over time, able to converge to a meaningful result.

Automatic FWI Workflow

Salvus offers a workflow to perform full waveform inversion on all scales ranging from ultrasonic applications all the way to global seismology. A direct consequence is that every aspect must be highly configurable while still being able to run in a fully automatic fashion.

This is achieved via a Python based user-interface that allows fine-grained control and comes with a comprehensive suite of visualizations. Most images on this page are in fact screenshots of Salvus in action.

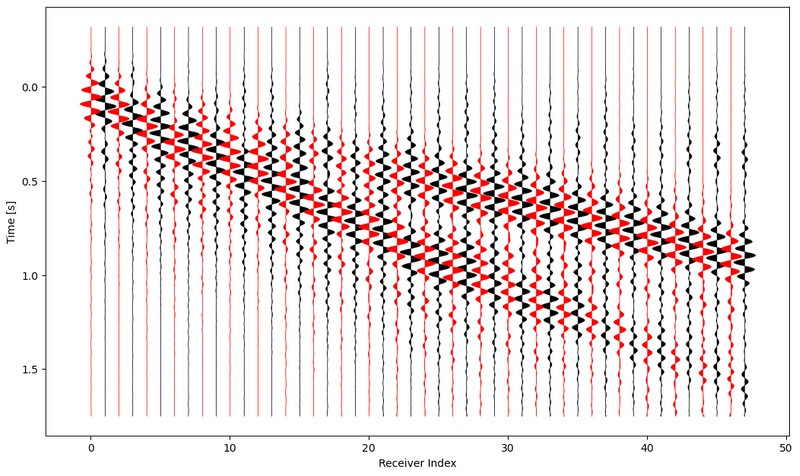
Results

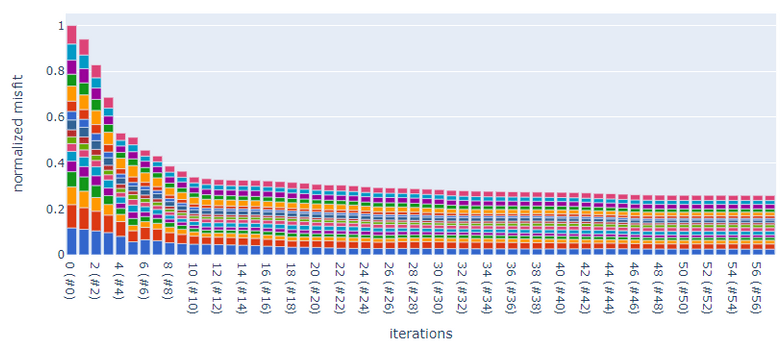
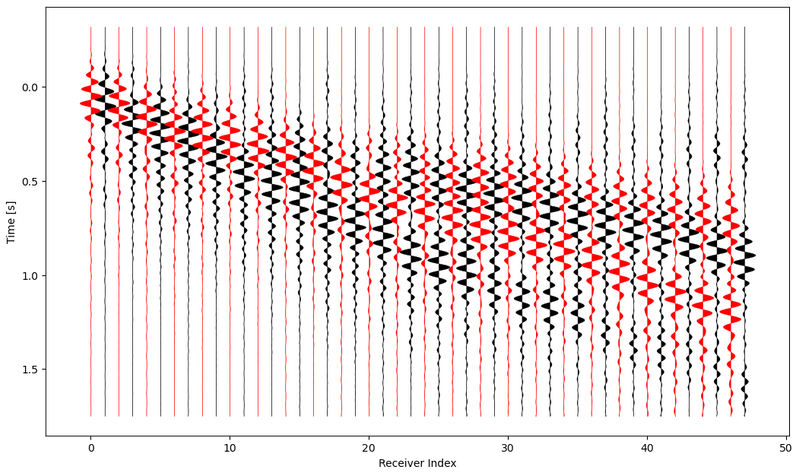
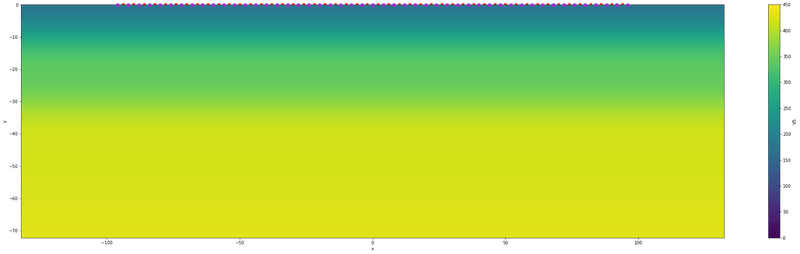
We ran a heavily regularized visco-elastic inversion for 56 iterations with a trust-region L-BFGS optimization method starting from a very rough 1-D model. The misfit drops significantly and the final model is able to explain all major features of the observed data while the model stays free from obvious over-fitting artifacts.

Figure: A graphical representation of the misfit in the course of this inversion.

Figure: Interleaved shotgather plots of the data (observed) versus the synthetics (red) of the initial model (on the left) and of the final model (on the right). The synthetic data of the initial model are highly cycle skipped and would ordinarily require careful data selection but the chosen optimal transport misfit fully solves this issue. As can be seen on the right hand side, the synthetics through the final model can represent the field data very well.

Figure: The initial (left) and final (right) isotropic S-wave velocity model. We started with a simplistic smoothed 1-D model derived from a SASW study and used scaling relations for the remaining parameters. The final model is heavily regularized but shows much lower velocities close to the surface and an embedded slower layer. Sources and receivers are shown as red and purple dots on the surface.

Interested?

This page naturally omits a lot of details. If you want to learn more please head over to Salvus' documentation for details regarding the technical and scientific background.